Summary¶
QCircuits is a Python package for the simulation and study of quantum computers based on the quantum circuit model. It has been designed to have a simple, lightweight interface and to be easy to use, particularly for those new to quantum computing.
Documentation, tutorial, and examples¶
Installation¶
Install with pip:
pip install qcircuits
or from the source at github.com/grey-area/qcircuits.
Example usage: quantum teleportation¶
See the examples page for more examples.
Quantum circuit:
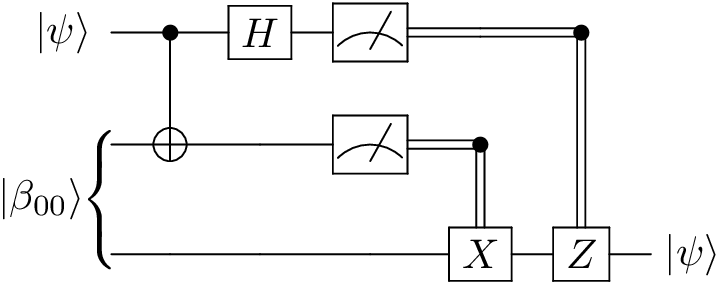
Code:
import qcircuits as qc
# Quantum Teleportation: transmitting two classical bits to transport a qubit state
# Alice has a qubit in a given quantum state.
# Alice and Bob have previously prepared a Bell state, and have since
# physically separated the qubits.
# Alice manipulates her hidden qubit and her half of the Bell state, and then
# measures both qubits.
# She sends the result (two classical bits) to Bob, who is able to reconstruct
# Alice's state by applying operators based on the measurement outcomes.
def quantum_teleportation(alice_state):
# Get operators we will need
CNOT = qc.CNOT()
H = qc.Hadamard()
X = qc.PauliX()
Z = qc.PauliZ()
# The prepared, shared Bell state
bell = qc.bell_state(0, 0)
# The whole state vector
state = alice_state * bell
# Apply CNOT and Hadamard gate
state = CNOT(state, qubit_indices=[0, 1])
state = H(state, qubit_indices=[0])
# Measure the first two bits
# The only uncollapsed part of the state vector is Bob's
M1, M2 = state.measure(qubit_indices=[0, 1], remove=True)
# Apply X and/or Z gates to third qubit depending on measurements
if M2:
state = X(state)
if M1:
state = Z(state)
return state
if __name__ == '__main__':
# Alice's original state to be teleported to Bob
alice = qc.qubit(theta=1.5, phi=0.5, global_phase=0.2)
# Bob's state after quantum teleportation
bob = quantum_teleportation(alice)
print('Original state:', alice)
print('\nTeleported state:', bob)